A game in a pure language (part 2): state
My first post about this project was a general introduction and an overview of my impressions of Idris. In this one, I’ll go over some elementary facilities that enable creating stateful systems like games in a pure language. Also I finally published the game’s source code: github.com/corazza/game-idris (it’s last been tested in Idris 1.3.1).
A pure language has no implicit state or side effects (i.e. you can’t just take user input, mutate a variable such as health, and blit things to the screen directly), while games are programs that seem to be all about state, side effects, interactivity… Well, it turns out that explicit state and side effects, which pure languages can operate with, are good enough! But I didn’t really know much about that when starting this project.
I had some minimal Haskell knowledge, and while the Idris book does go over state management, the scope is mostly simple exercises where your state can be represented as a single Nat or something like that: definitely not a large system with multiple moving parts coming in and out of existence. The accent was definitely on correctness rather than performance and practical implementations.
Still though, those exercises really do form the basic building blocks that you need to understand before dealing with larger systems, so I’ll present two of them from the Idris book, along with Control.ST which is an out-of-the-box facility putting those ideas into practice:
Example 1: basic stateful operations in Haskell / Idris
A good starting example is a tree-labelling program, where the goal is to label each node of a binary tree in some order:
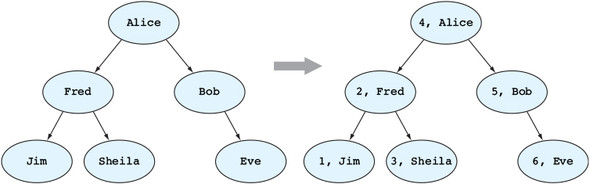
This is a good way to introduce state in functional programming because at first you’d naively reach for a stateless recursive solution to the problem. Which of course, exists and works, but is a bit convoluted and harder to scale into larger solutions:
treeLabelWith : (lbls : Stream labelType) ->
(tree : Tree a) ->
(Stream labelType, Tree (labelType, a))
treeLabelWith lbls Empty = (lbls, Empty)
treeLabelWith lbls (Node left val right)
= let (lblThis :: lblsLeft, left_labelled) = treeLabelWith lbls left
(lblsRight, right_labelled) = treeLabelWith lblsLeft right
in
(lblsRight, Node left_labelled (lblThis, val) right_labelled)
The problem here is in the return type, (Stream labelType, Tree (labelType, a)): we don’t just return the labeled tree, but a new stream of labels. This is necessary because when labelling the left child recursively, we don’t know how many labels were consumed, so when resuming to label the root and the right child, we needed to be explicitly told where to continue from by the left-child recursive call. Of course, you can wrap this later, but the implementation isn’t really elegant.
A better solution would be to use Control.Monad.State in order to weave in an explicitly-stateful list of labels, allowing us to write nicer-looking code:
-- input -> State (state type) (return type of stateful computation)
treeLabelWith : Tree a -> State (Stream labelType) (Tree (labelType, a))
treeLabelWith Empty = pure Empty
treeLabelWith (Node left val right)
= do left_labelled <- treeLabelWith left
(this :: rest) <- get
put rest
right_labelled <- treeLabelWith right
pure (Node left_labelled (this, val) right_labelled)
treeLabel : Tree a -> Tree (Integer, a)
treeLabel tree = evalState (treeLabelWith tree) [1..]
Now the implementation of labelling is more readable, because we don’t have to drag the state (labels) around explicitly. This is just an example of composing stateful operations, and it may appear that not much was achieved by modifying this isolated labelling function, however in a larger program writing this kind of monadic code is the only practical way to compose the system.
Example 2: verified state transitions
Imagine you’re programming an ATM. Such a machine obviously needs a high degree of assurance in its code’s correctness, so that you can’t e.g. give out money before the PIN has been checked, don’t eject a card when there is none inserted, etc. The cost of getting these state transitions wrong can be high, so in most other languages you’d invest in a variety of methods to proof it most of which in the end cash out in expensive work-hours. But whatever methods you eventually end up using, they will be lacking in a crucial aspect: they will never give complete assurance about the implementation, the code itself. The compiler will detect some bugs, the runtime, if it has a larger presence, will help in handling certain kinds of errors, but at the end of the day imperative languages and most pure functional ones rely on the programmer to correctly write the algorithm and differ only in degree with regards to the amount of help offered.
But Idris is different. Instead of trying to be really sure the implementation of your ATM is correct through external methods, dependent typing in Idris lets you encode state transitions in types, meaning that the compiler can formally prove, for each of your functions that handles the ATM’s state, that it does so according to rules that had been laid out before. This means that it’s impossible to compile code in which some minor, misplaced call in an infrequent branch messes up the ATM state.
Here’s how these state transitions are specified:
PIN : Type
PIN = Vect 4 Char
data ATMState = Ready | CardInserted | Session
data PINCheck = CorrectPIN | IncorrectPIN
-- commands that are composed into ATM-handling programs:
-- READ AS return type -> begin state -> f computing the resulting state -> give an ATM command
data ATMCmd : (ty : Type) -> ATMState -> (ty -> ATMState) -> Type where
InsertCard : ATMCmd () Ready (const CardInserted)
GetPIN : ATMCmd PIN CardInserted (const CardInserted)
CheckPIN : PIN -> ATMCmd PINCheck CardInserted
(\check => case check of
CorrectPIN => Session
IncorrectPIN => CardInserted)
-- ... other commands, for example logging ...
The above snippet is part of a definition of a data type whose values are ATM commands, which are composed into ATM programs. The line GetPIN : ATMCmd PIN CardInserted (const CardInserted) means that GetPIN is a value representing an ATM command which returns a PIN, begins in the state CardInserted, and no matter what (const) remains in the CardInserted state. Now, were you to call (bind, more accurately) this GetPIN value while the ATM was in Ready state, the program wouldn’t compile!
CheckPIN is more interesting, however, because it showcases more of the mechanism enabling verification of complex state transitions.
CheckPIN : PIN -> ATMCmd PINCheck CardInserted
(\check => case check of
CorrectPIN => Session
IncorrectPIN => CardInserted)
Firstly, CheckPIN is a function which takes a PIN and returns an ATM command. That ATM command itself returns a PINCheck value–either CorrectPIN or IncorrectPIN, and has to start in the CardInserted state. Where things get interesting is that last constructor argument. In the prior two ATM commands, this was just const some_state, meaning a function which always evaluated to the same specified ATM state. The reasoning there was obvious: inserting a card gets us into the CardInserted state no matter what, and getting the PIN never changes the state from CardInserted.
But CheckPIN is different, in the sense that it represents a conditional state transition! Whether the ATM remains in the CardInserted state or moves into the Session state depends on the resulting PINCheck! The practical result of this is that you are forced to match on the result, and the different branches of the match expression will have different types depending on this value: if you try executing a command that expects the operation to have succeeded, it wouldn’t typecheck unless it’s in the correct branch.
Here’s a much less complicated snippet which shows how this ATMCmd type is used:
atm : ATMCmd () Ready (const Ready)
atm = do InsertCard
pin <- GetPIN
pinOK <- CheckPIN pin
case pinOK of
CorrectPIN => do cash <- GetAmount
Dispense cash
EjectCard
IncorrectPIN => EjectCard
I believe this code is rather beautiful and simple: there are no implementation details whatsoever, only logic–correct logic! All ATM programs care about is that they’re values of the type ATMCmd, that is, that they’re composed in a way that respects certain rules defined in their type.
Now all that is left is defining the implementation of ATMCmd values, a function called runATM for example, which takes an ATMCmd and ‘runs’ it. ‘Run’ in this context could mean several things, but in this example it means a mapping from ATMCmd ty in out to IO ty. But it could also mean a mapping from ATMCmd ty in out to ATM_internal ty, where ATM_internal is some special monad for communicating with the actual ATM machinery in a restricted, controlled manner. An example runATM:
runATM EjectCard = putStrLn "Card ejected"
runATM GetPIN = do putStr "Enter PIN: "
readVect 4
-- ...
That’s all there is to the implementation! The EjectCard case is especially curious, because you’d expect something that actually changes a state. But that’s part of the type specification! So the only thing left for the implementation is displaying a message. (In the real-world scenario we’d also call a function that would cause the ATM to eject the card.)
This is separation of logic and implementation to a quite high degree, and is a frequent pattern in stateful Idris code. When I wrote the scripting part of the game, I used something like this: there is a RuleScript monad which is simple and nice to write in, and there is a runScript function that maps its values into some lower-level representations (game state changes).
STrans and ST
The last exercise was about creating a custom type in order to model a stateful system and operations on it. That is an oft-repeated pattern, and STrans and its helper type constructor ST generalize it.
Lets look at ATMCmd again to see which parts generalize.
data ATMCmd : (ty : Type) -> ATMState -> (ty -> ATMState) -> Type where
It is a type constructor taking the following arguments:
ty : Type: the return type of the ATM operationATMState: a value of this type (Ready | CardInserted | Session) that represents the initial state the ATM is in(ty -> ATMState): a function from the return type toATMState, representing how the state of the ATM changes depending on the result of the operation
The result is a Type. For example ATMCmd () Ready (const CardInserted) is the type of the value InsertCard, which means that InsertCard:
- is an ATM operation which returns the unit value,
- has to begin in the
Readystate, and - always ends in
CardInsertedstate
The function (well, value) atm has type ATMCmd () Ready (const Ready): it is the main ATM program, and its type means that an ATM always begins and ends in a Ready state–that this is actually respected by our implementations is guaranteed by the Idris compiler.
Again–what generalizes here? A lot! It turns out that many stateful programs can be composed from values that represent operations of a similar kind: they can return a value, there are preconditions (for example an ATMState), and a function representing the postconditions of the operation. There are also functions that can utilize this type to compose two operations, respecting the proper chaining of the preconditions and postconditions. Of course this is what >>= does. (It was also defined for ATMCmd, but I left it out, you can see the code here: TODO LINK HERE)
This is pretty much what the type constructor STrans represents:
data STrans : (m : Type -> Type) -> (ty : Type) -> Resources -> (ty -> Resources) -> Type
There are two major differences: m : Type -> Type and Resources. Let’s explain them in order.
The context, m : Type -> Type
(For initial intuition, let m = IO. It at least makes sense: m and IO have the same type, Type -> Type.)
This is the biggest difference between hand-crafted implementations of stateful types like ATMCmd and STrans, but it’s very simple and logical. Lets introduce some motivation: say that you want to do some basic logging to stdout from your ATMCmd programs. How would you do that? You can’t just pepper it with putStrLn, that only works in IO! You could add a Log function in the interface definition. Indeed that would work, but for anything else that you wanted to do, you’d have to implement a custom constructor. You could generalize this further, but at that point, it becomes sensible to do exactly what STrans does: introduce the notion of a context that your operations run in.
The main thing you can do with a context is lift values from it into your own type. Effectively this transforms a value like IO Int into a value like ATMCmd Int .... So instead of directly calling putStrLn, which cannot be done, or implementing Log yourself, you can now just use a lift putStrLn. This is no longer a function in the IO monad, but a function that produces a value that fits your own type.
Resources
I won’t delve into the technical details here. STrans lets you create, update, and destroy resources which hold your state. Instead of just using a sum type for your state to describe its preconditions and postconditions, with resources the idea is that you store something quite complex (like the state of the game!) and assert its presence, something about it, update it, delete it, etc.
This is how you get something like “memory management”: if your program begins and ends without resources, then any resources you create, you must respectively destroy.
You can see this in action in this part of the code that begins and ends the game’s physical world:
startDynamics settings = with ST do
world <- lift $ createWorld $ gravity settings
-- create the physical state:
pdynamics <- new (pdynamicsInStart world (timeStep settings))
pure pdynamics
endDynamics dynamics = with ST do
dynamics' <- read dynamics
lift $ destroyWorld (world dynamics')
-- destroy the physical state:
delete dynamics
This is where the ST constructor also appears. It’s pretty much just a convenience, letting you write less verbose code. Instead of specifying a list of resources, and a function that computes the resulting list of resources, you can specify a list of resource transitions. As an example, the types of the above functions:
startDynamics : (settings : DynamicsSettings) -> ST m Var [add SDynamics]
endDynamics : (dynamics : Var) -> ST m () [remove dynamics SDynamics]
add and remove are functions that specify these resource transitions on the type level. The return type of startDynamics is Var, which TODO
So how does this all fit together?
The general idea was to split game state up into stateful systems along concern boundaries, mainly, Server, Client, and Dynamics (wrapper around the physics engine). The server owns the game logic and sends authoritative updates to the client; the client updates some internal states (e.g. for animation), processes SDL2 events and send the results to the server, and owns the UI and rendering logic. The ‘dynamics’ component, aside from owning the simulation and positional data of objects in the game, is also responsible for control logic (i.e. enabling movement, jumping) and producing physics-related events (collisions, query results).
All three of these major components are implemented as interfaces utilizing ST over some general context m. As seems to be idiomatic Idris, they have a single abstract implementation for any context that satisfies certain constraints. For example:
interface Server (m : Type -> Type) where
-- ...
And the implementation:
(GameIO m, Rules m) => Server m where
This means that if you want to call functions defined under the Server interface, your context m must necessarily have implementations of GameIO and Rules (practically, this enables the implementation of Server to call functions in GameIO and Rules).
The implementation of these subsystems, however, is largely not done inside stateful ST code. Most of it is implemented through query and update functions, operating on regular Idris data structures, that describe “atomic” operations which the stateful part of the code just glues together. Here’s an example stateful method that creates a physical object in the game:
createObject server creation object_description = with ST do
id <- decideId server creation
case createObjectCommand creation object_description id of
Left e => pure $ fail $ e ++ " (createObject server)"
Right command => with ST do
updatePServer server $ addDynamicsCommand command
updatePServer server $ addInSessionCommand $ Create id (ref creation) (render creation)
addRules server id object_description creation
pure $ Right id
While there are purely stateful operations called directly, such as decideId, most changes to the server state are done through the updatePServer operation (P stands for pure), which is a simple operation that takes a pure update (PServer -> PServer) and applies it to the server state. Then, helper functions can be written in a pure style to produce these PServer -> PServer updates. All major components are written in this manner.
That’s all for this post. Next, I hope to cover my favorite part: scripting.